Info
- Title: Adversarially Learned Inference
- Task: Image Generation
- Author: Vincent Dumoulin, Ishmael Belghazi, Ben Poole, Alex Lamb, Martin Arjovsky, Olivier Mastropietro and Aaron Courville
- Date: June 2016
- Arxiv: 1606.00704
- Published: ICLR 2017
Abstract
We introduce the adversarially learned inference (ALI) model, which jointly learns a generation network and an inference network using an adversarial process. The generation network maps samples from stochastic latent variables to the data space while the inference network maps training examples in data space to the space of latent variables. An adversarial game is cast between these two networks and a discriminative network is trained to distinguish between joint latent/data-space samples from the generative network and joint samples from the inference network. We illustrate the ability of the model to learn mutually coherent inference and generation networks through the inspections of model samples and reconstructions and confirm the usefulness of the learned representations by obtaining a performance competitive with state-of-the-art on the semi-supervised SVHN and CIFAR10 tasks.
Motivation & Design
The adversarially learned inference (ALI) model is a deep directed generative model which jointly learns a generation network and an inference network using an adversarial process. This model constitutes a novel approach to integrating efficient inference with the generative adversarial networks (GAN) framework.
What makes ALI unique is that unlike other approaches to learning inference in deep directed generative models (like variational autoencoders (VAEs)), the objective function involves no explicit reconstruction loop. Instead of focusing on achieving a pixel-perfect reconstruction, ALI tends to produce believable reconstructions with interesting variations, albeit at the expense of making some mistakes in capturing exact object placement, color, style and (in extreme cases) object identity. This is a good thing, because 1) capacity is not wasted to model trivial factors of variation in the input, and 2) the learned features are more or less invariant to these trivial factors of variation, which is what is expected of good feature learning.
These strenghts are showcased via the semi-supervised learning tasks on SVHN and CIFAR10, where ALI achieves a performance competitive with state-of-the-art.
Even though GANs are pretty good at producing realistic-looking synthetic samples, they lack something very important: the ability to do inference.
Inference can loosely be defined as the answer to the following question:
Given x, what z is likely to have produced it?
This question is exactly what ALI is equipped to answer.
ALI augments GAN’s generator with an additional network. This network receives a data sample as input and produces a synthetic z as output.
Expressed in probabilistic terms, ALI defines two joint distributions:
- the encoder joint $q(\mathbf{x}, \mathbf{z}) = q(\mathbf{x})q(\mathbf{z} \mid \mathbf{x})$ and
- the decoder joint $p(\mathbf{x}, \mathbf{z}) = p(\mathbf{z})p(\mathbf{x} \mid \mathbf{z})$.
ALI also modifies the discriminator’s goal. Rather than examining x samples marginally, it now receives joint pairs $(x, z)$ as input and must predict whether they come from the encoder joint or the decoder joint.
Like before, the generator is trained to fool the discriminator, but this time it can also learn $q(z∣x)$.
The adversarial game played between the discriminator and the generator is formalized by the following value function:
In analogy to GAN, it can be shown that for a fixed generator, the optimal discriminator is
and that given an optimal discriminator, minimizing the value function with respect to the generator parameters is equivalent to minimizing the Jensen-Shannon divergence between $p(x,z)$ and $q(x,z)$.
| Matching the joints also has the effect of matching the marginals (i.e., $p(x) \ sim q(x)$ and $p(z) \sim q(z)$) as well as the conditionals /posteriors (i.e., $p(z | x) \sim q(z | x)$ and $q(x | z) \sim p(x | z)$). |
Experiments & Ablation Study
CIFAR10
The CIFAR10 dataset contains 60,000 32x32 colour images in 10 classes.
 |
 |
|---|---|
| Samples | Reconstructions |
SVHN
SVHN is a dataset of digit images obtained from house numbers in Google Street View images. It contains over 600,000 labeled examples.
 |
 |
|---|---|
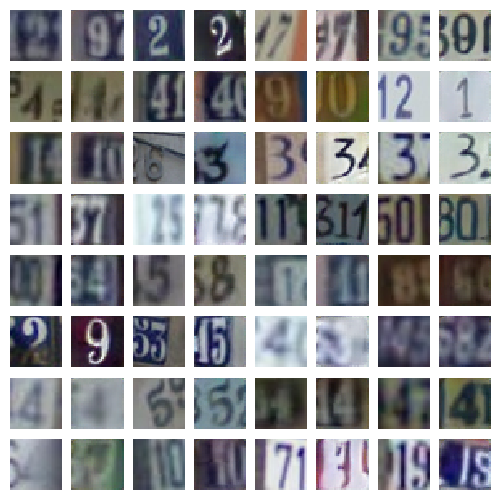| Samples | Reconstructions |
CelebA
CelebA is a dataset of celebrity faces with 40 attribute annotations. It contains over 200,000 labeled examples.
 |
 |
|---|---|
| Samples | Reconstructions |
Tiny ImageNet
The Tiny Imagenet dataset is a version of the ILSVRC2012 dataset that has been center-cropped and downsampled to 64×6464×64 pixels. It contains over 1,200,000 labeled examples.
 |
 |
|---|---|
| Samples | Reconstructions |